Balancing Quality ISO 21940 (1940)
Welcome to next Adash video about balancing and the ISO 1940 (ISO 21940) standard. The text of 1940 standard is quite difficult to read. I am sure that many of you tried to read it and you gave it up. In this video I simplify the text of the ISO 1940 (ISO 21940) standard..
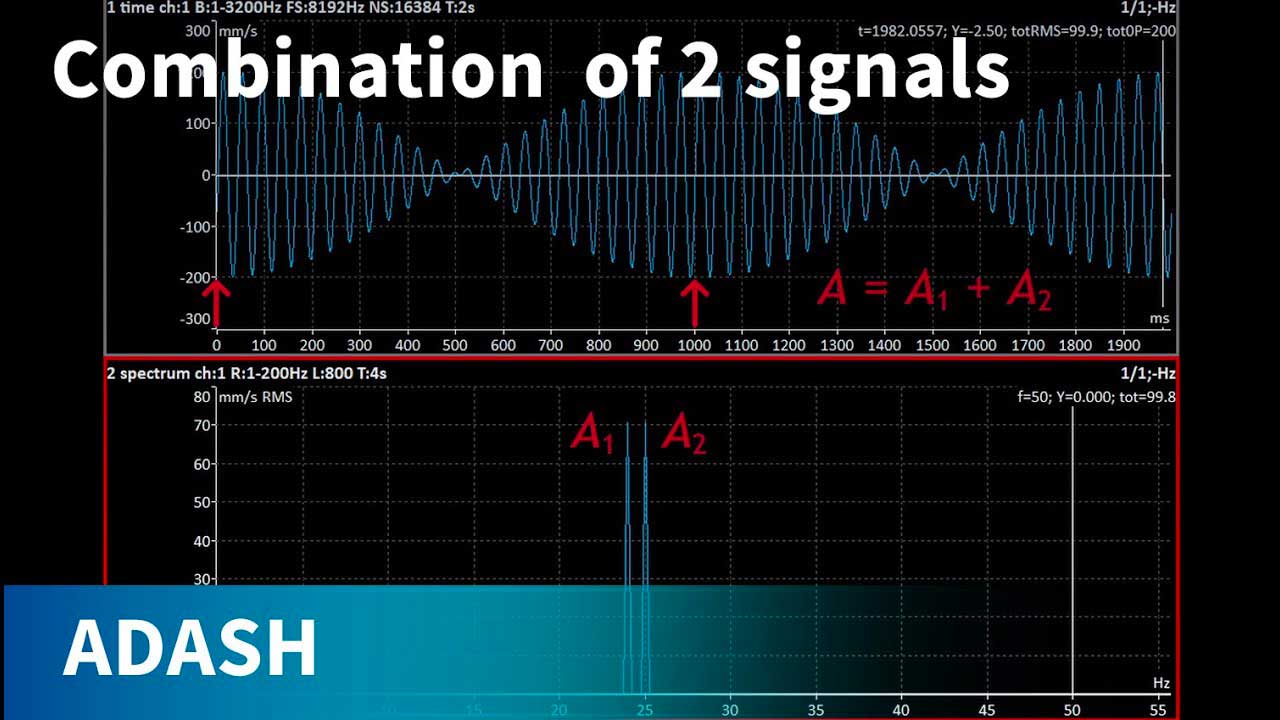
What is the balance quality? It is what the standard describes. Usually all of us use the vibration level as balance quality. If vibrations are low, then we are satisfied. But the standard uses other concept..
For example we have rotor with zero unbalance. I mount the mass to some position. The question is : "Can I run and use this machine with this heavy spot?" Is it the unbalance acceptable for safe run? By other words, I would like to know how massive the heavy point can be to allow the machine be running..
By next other words , what is the acceptable or permissible residual unbalance? To obtain a satisfactory running of the rotor, the residual unbalance Ures should not be higher than a permissible value Uper..
What is the unit for Uper? The SI unit is kg times meter, but more practical is g times mm. I will explain it later. It describes the heavy spot. It tells us that specific mass is mount on specific radius..
When the rotor is running, then centrifugal force is created. And this force hurts us. It causes bearing damage. The formula is this. Force F is equal mass m times radius r times square of angular velocity omega. You can see that double mass doubled the force. The double radius also doubled the force. The omega is the speed. You can see the square root of that. It means two times higher speed creates four times higher force..
Now short explanation of radian. When we talk about angles, we use the degrees as the unit. You know that the circle has 360 degrees. I can say that one rotation has 360 degrees. But also radian unit exist for angle value. One rotation is 2 * π radians. Now we know that one circle has 360 degrees or 2 * π radians. You can simply derive, that 1 radian is equal 57.3 degrees. Now you know, that we have two units for angle measurement. The degree and the radian..
The omega is angular velocity, the radian per second is the unit. It is rotation speed. We use the speed in Hz usually. It is the number of rotations per second. And we can easily convert the angular velocity omega to Hz. The formula is that omega is equal 2 times pi times frequency in Hz. One rotation omega is equal 2 * π. When we need f rotations per second, then we must multiply it by f..
Now about the relation of permissible residual unbalance and rotor mass. Look at rotor on picture, for example the permissible residual unbalance is 100 000 g mm. I can re-calculate it to 100 g m. Now I add the same next rotor to this one. This new one has the same individual permissible residual unbalance two times heavier rotor has two times higher permissible residual unbalance. .
In general, for rotors of the same type, the permissible residual unbalance Uper = eper * rotor mass (kg). We must multiplay the eper by mass. Uper is proportional to the rotor mass. It means I can use this value for next calculations. It is relative value which depends on rotor mass. It is called permissible residual specific unbalance eper..
The rotor has the geometrical center just in the middle of the circle. When it is perfectly balanced, then also center of gravity is in the same position. Now I added heavy spot. The center of gravity moves. I can measure the distance between geometrical center and center of gravity in micrometers..
That it is the reason, why we use this units for eper. We can work with this fraction. Kg is equal 1000 times gram. Now we can shorten the grams. We get mm divided by 1000. And it is the micrometer. It means the eper is the permissible distance between geometrical center and center of gravity in micrometers for rotor mass one kilogram..
We are used to using RPM or Hz for speed. Not the radians, which is better for calculations. The circumference of a circle with radius one is two π. When the speed is 1 Hz, then this 2 π rotation must be done in 1 second. It means the angular speed omega is equal 2 π. When speed is higher, then the angular speed omega is equal 2 π times speed frequency in Hz. .
And what about the rotor speed. The iso 1940 tells this. Experience shows that for rotors of the same type the permissible residual specific unbalance value eper varies inversely with the speed of the rotor. It is not derived just from experience. This corresponds exactly to the laws of physics..
Differently expressed, this relationship is given by the following equation, eper multiplied by Ω is constant value. It means for two times higher speed we get two times lower permissible residual specific unbalance eper. The question is how big is the constant value?